안녕하십니까 힘법사입니다. 오늘은 JPEG 압축 과정 중 하나로 들어가는 DCT, IDCT, Quantization, De-Quantization에 대한 내용을 설명드리도록 하겠습니다. 사실 제가 실감미디어시스템이라는 학교 수업을 들으면서 진행한 내용인데, 코드 작성과 보고서 둘다 진행하게 되어 이렇게 공유하게 되었습니다. 내용은 보고서 내용을 그냥 그대로 올려봤고요 이미지에 대한 DCT과정이 동작되는 코드는 아닌 오직 8x8 마크로 블록에만 적용되도록 만든 코드입니다.
많이 어려운 내용은 아니니 따라오시면 이해하실 수 있을겁니다~!
먼저 코드 링크부터 걸겠습니다.
2017103030/DCT: DCT, IDCT, Quantization, DeQuantization operation code (github.com)
GitHub - 2017103030/DCT: DCT, IDCT, Quantization, DeQuantization operation code
DCT, IDCT, Quantization, DeQuantization operation code - GitHub - 2017103030/DCT: DCT, IDCT, Quantization, DeQuantization operation code
github.com
I. 코드의 목적
1, DCT를 구현 및 실습
DCT는 변환 결과물이 복소수로 나오는 DFT와는 다르게 결과가 실수로만 구성되어있다. 고로 처리하기가 간편하다. 이런 특성 때문에 신호 및 영상처리에 많이 사용된다. 에너지 성분이 대부분 저주파에 집중되기 때문에 Lossy compression(손실 압축)에 자주 사용된다.
실습에서는 DCT를 구현해 적용해보았을 때 실제로 저주파 성분에 에너지가 많이 집중되는지 확인할 수 있다.
2. Quantization 실습
DCT로의 변환만으로는 압축이 일어나지 않는다. Quantization을 구현하고 실습 결과를 통해 Quantization 시 RLC이 유리한 이유를 관찰한다.
3. IDCT를 구현 및 실습
원본 데이터에 DCT와 Quantization 후 변환 데이터에 역과정인 De-Quantization 과정과 IDCT를 적용했을 때 원본 데이터와 유사한 데이터가 얻어지는지 관찰한다.
II. 과정
Class DCT 설명
“I.과제의 목적”에 해당하는 실습과정을 수행하기위해 C++에서 Class Dct를 직접 제작하여 이를 통해 실습을 진행하였다.
Class DCT는 정해진 Macro block에 대해 DCT와 IDCT 그리고 Quantization과 이에 역 과정에 해당하는 De-Quantization 연산을 지원하는 Class다.
전체 클래스의 뷰는 그림1과 같이 확인할 수 있다. 총 네 개의 멤버 변수 및 배열로 이루어져 있고, 12개의 멤버 메소드가 구현되어 있다. 멤버 변수는 표1의 설명과 같이 구성되어 있다.
| 변수 | 설명 |
| -m_blocksize : int | 마크로 블록의 크기를 나타내는 변수 |
| -m_Fuv : int** | DCT 결과를 저장하는 배열 |
| -m_recovery : unsigned char** | 복구된 데이터를 저장하는 배열 |
| -m_yplane : unsigned char** | 원본 데이터 / LuminancePlane 값을 저장하는 배열 |
표1 Dct 클래스 멤버 변수 설명 표

총 멤버 함수의 종류는 12가지로 대부분의 함수의 주 동작 목적은 DCT, IDCT Quantization, De-Quantization 기능에 초점이 맞춰져 있다.
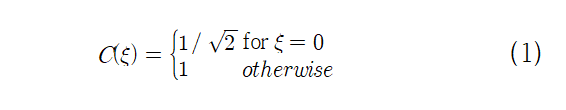
수식 1은 상수 C가 어떻게 결정되는지 보여준다. 상수 C는 수식4 DCT 과정과 수식3 IDCT 과정에 사용되고 Dct Class에서는 float ConstC(int) 함수로 구현되어 있다.

수식 2는 DCT 연산에서 시그마 합 연산만을 취급하는 수식이다. 해당 연산은 수식(4) DCT 연산에 사용되고 Dct Class에서는 float DctSigma(int,int) const 함수로 구현되었다.
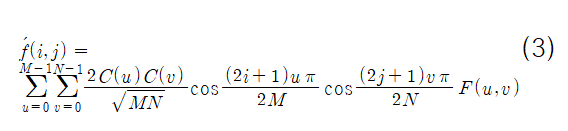
수식3은 IDCT 연산이다. 해당 수식은 특정 (i,j)에 대한 수식3의 결과를 도출하는 float IdctSigma(int,int) const 함수와 IdctSigma(int,int) 함수의 결과를 이용해 모든 가능한 (i,j)에 대한 연산을 수행해 결과적으로 IDCT 결과를 수행하고 저장하는 void InvTransform() 함수에 사용되었다.
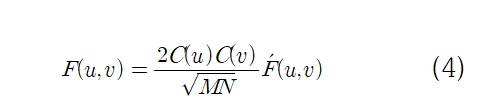
수식4는 DCT 연산의 수식을 나타내고 Dct Class에서 void Transform 함수로 구현되었다. 그 외 모든 Dct 클래스의 멤버 함수는 표2에 기능과 함께 정리하였다.
| 함수 | 설명 |
| +Dct(int) | macro block의 크기를 초기화하고 향후 연산에 필요한 메모리 공간을 할당한다. |
| +~Dct() | 할당한 메모리 공간을 모두 반환한다. |
| -ConstC(int) const : float | 수식(1)에 따라 결과값을 반환한다. |
| -DctSigma(int, int) const : float | 수식(2)에 따라 결과값을 반환한다. |
| -IdctSigma(int, int) const : float | 수식(3)에 따라 결과값을 반환한다. |
| +ShiftLuminancePlane(int,int) : void | int ** m_yplane 즉 Luminance Plane 배열에 일정한 값을 더해주거나 빼주는 함수로 동작한다. |
| +ReadMat(unsigned char **&input) : void | 외부의 unsigned char** 배열을 읽어 Class의 멤버 배열 m_yplane에 저장한다. |
| +Transform() : void | DCT 연산을 수행한다. 계산 결과는 수식(4)에 따라 진행되며 int ** m_Fuv 배열에 저장된다. |
| +Quantizationing() : void | int ** m_Fuv 배열에 미리 준비된 quantization table의 값으로 모든 원소의 몫을 취해 int ** m_Fuv에 저장한다. |
| +InvTransform() : void | IDCT 연산을 수행한다 .계산 결과는 수식(5)에 따라 진행되며 결과는 m_recovery 배열에 저장된다. |
| +InvQuantizationing() : void | int ** m_Fuv 배열에 미리 준비된 quantization table의 값으로 모든 원소에 곱을 취해 int ** m_Fuv에 저장한다. |
| +PrintMatrix(int) const : void | 입력에 따라 객체의 멤버배열인 m_yplane, m_Fuv, m_recovery, Error Matrix를 출력한다. |
표2 Dct 클래스 멤버함수 종류
2. 예제 블록 읽기 및 Shift 단계
우선 예제 블록을 표3과 같이 준비한다. 해당 블록을 Dct Class에 ReadMat 함수를 이용해 멤버 배열에 저장한 후, -128만큼 값들을 이동시키기 위해 ShiftLuminancePlane 함수를 호출해 해당 값들을 –128만큼 이동시킨다.
| 200 | 202 | 189 | 188 | 189 | 175 | 175 | 175 |
| 200 | 203 | 198 | 188 | 189 | 182 | 178 | 175 |
| 203 | 200 | 200 | 195 | 200 | 187 | 185 | 175 |
| 200 | 200 | 200 | 200 | 197 | 187 | 187 | 187 |
| 200 | 205 | 200 | 200 | 195 | 188 | 187 | 175 |
| 200 | 200 | 200 | 200 | 200 | 190 | 187 | 175 |
| 205 | 200 | 199 | 200 | 191 | 187 | 187 | 175 |
| 210 | 200 | 200 | 200 | 188 | 185 | 187 | 186 |
표3 Dct 실습을 위한 예제 블록
-128만큼 이동시키게 되면 블록은 표4와 같은 상태로 나타나게 된다.
| 72 | 74 | 61 | 60 | 61 | 47 | 47 | 47 |
| 72 | 75 | 70 | 60 | 61 | 54 | 50 | 47 |
| 75 | 72 | 72 | 67 | 72 | 59 | 57 | 47 |
| 72 | 72 | 72 | 72 | 69 | 59 | 59 | 59 |
| 72 | 77 | 72 | 72 | 67 | 60 | 59 | 47 |
| 72 | 72 | 72 | 72 | 72 | 62 | 59 | 47 |
| 77 | 72 | 71 | 72 | 63 | 59 | 59 | 47 |
| 82 | 72 | 72 | 72 | 60 | 57 | 59 | 58 |
표4 -128만큼 이동 후 블록 상태

그림2는 시스템 동작 시 출력되는 화면을 보여준다. 예제 블록에 대한 로드 과정과 –128만큼의 값 이동 과정이 올바르게 이뤄졌음을 확인할 수 있다.
3. DCT, Quantization 수행 단계
과정2에서 얻은 블록에 대해 DCT를 수행할 수 있다, DCT 연산식은 수식4와 같고 Dct Class의 Transform 함수를 호출함으로서 계산이 이뤄진다.
| 515 | 65 | -12 | 4 | 1 | 2 | -8 | 5 |
| -16 | 3 | 2 | 0 | 0 | -11 | -2 | 3 |
| -12 | 6 | 11 | -1 | 3 | 0 | 1 | -2 |
| -8 | 3 | -4 | 2 | -2 | -3 | -5 | -2 |
| 0 | -2 | 7 | -5 | 4 | 0 | -1 | -4 |
| 0 | -3 | -1 | 0 | 4 | 1 | -1 | 0 |
| 3 | -2 | -3 | 3 | 3 | -1 | -1 | 3 |
| -2 | 5 | -2 | 4 | -2 | 2 | -3 | 0 |
표5 DCT 결과
표5는 표4의 상태에서 DCT를 수행한 결과이다.
| 16 | 11 | 10 | 16 | 24 | 40 | 51 | 61 |
| 12 | 12 | 14 | 19 | 26 | 58 | 60 | 55 |
| 14 | 13 | 16 | 24 | 40 | 57 | 69 | 56 |
| 14 | 17 | 22 | 29 | 51 | 87 | 80 | 62 |
| 18 | 22 | 37 | 56 | 68 | 109 | 103 | 77 |
| 24 | 35 | 55 | 64 | 81 | 104 | 113 | 92 |
| 49 | 64 | 78 | 87 | 103 | 121 | 120 | 101 |
| 72 | 92 | 95 | 98 | 112 | 100 | 103 | 99 |
표6 Quantization table
표6은 Quantization Table을 보여준다. 표5의 블록에 대해서 동일한 인덱스에 원소에 대해서 Quantization table 값을 나눠 몫을 계산해 Quantization을 진행한다.
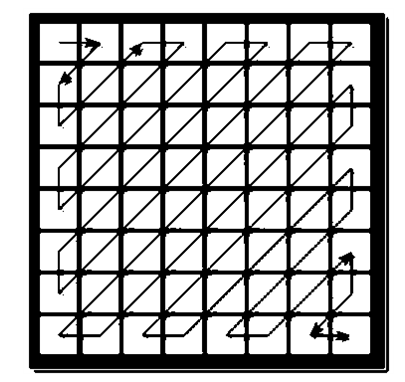
표7은 DCT 결과에 Quantization을 수행한 결과를 보여준다. DCT만 수행했을 때는 값에 0이 거의 없다. 하지만 Quantization 후 Zig-Zag 스캐닝을 활용한 RLC(Run Lenght Coding) 진행 시 큰 이점이 있을 것으로 알 수 있다. 8x8 블록에서 Zig-Zag 스캐닝이 이뤄지는 순서는 그림 4와 같다.
실제로 표7의 행렬에 대해 Zig-Zag 스캔과 RLC 코딩 결과
(0,6),(0,-1),(1,-1),(3,-1),(2,1),(0,0) 으로 매우 간단하게 그림7의 8x8 행렬의 정보를 나타낼 수 있다.
그림 3은 C++에서 프로그램 내에서 DCT와 Qunatization 연산 호출 시 출력되는 결과를 보여준다. DCT와 Quantization 과정 모두 정상적으로 처리되었음을 확인할 수 있다.

| 32 | 6 | -1 | 0 | 0 | 0 | 0 | 0 |
| -1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| -1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
표7 Quantization 수행결과
4. De-Quantization, IDCT, Shift 단계
De-Qunatization의 경우 표5의 Quantization table과 표7 행렬의 Quantization 수행결과 행렬에 같은 인덱스 끼리 곱셈을 해주어 수행된다. 해당 동작은 Dct Class의 InvQuantizationing 함수를 통해 수행된다.
| 512 | 66 | -10 | 0 | 0 | 0 | 0 | 0 |
| -12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| -14 | 0 | 16 | 0 | 0 | 0 | 0 | 0 |
| -14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
표8 De-Quantization 수행 결과
표8은 De-Quantization 수행결과로 표5의 기존 값에 비해서 고주파 영역의 값들이 상당히 소거된 것을 확인할 수 있다.
해당 결과에 대해서 IDCT를 Dct Class 내의 InvTransform 함수를 호출해 수식3의 연산을 진행하고 다시 128만큼 Shift 해주면 표9와 같은 복구 값을 얻을 수 있다.
| 199 | 196 | 191 | 186 | 182 | 178 | 177 | 176 |
| 201 | 199 | 196 | 192 | 188 | 183 | 180 | 178 |
| 203 | 203 | 202 | 200 | 195 | 189 | 183 | 180 |
| 202 | 203 | 204 | 203 | 198 | 191 | 183 | 179 |
| 200 | 201 | 202 | 201 | 196 | 189 | 182 | 177 |
| 200 | 200 | 199 | 197 | 192 | 186 | 181 | 177 |
| 204 | 202 | 199 | 195 | 190 | 186 | 183 | 181 |
| 207 | 204 | 200 | 194 | 190 | 187 | 185 | 184 |
표9 IDCT 연산을 이용해 값을 복구한 결과
복구 값을 표 3의 기존 값과 비교하면 육안으로 거의 유사한 값인 것을 확인할 수 있다. 이에 대한 수치적인 해석은 다음 장인 결론에 담도록 하겠다.

III. 결론
DCT와 Quantization 연산 결과 표7에 해당하는 데이터를 획득할 수 있었다. 그리고 이에 대해 그림4의 Zig-Zag scan을 적용했을 때 얻을 수 있는 값은
(0,6),(0,-1),(1,-1),(3,-1),(2,1),(0,0)으로 12개의 수로 기존의 64개의 값으로 이뤄진 블록을 표현할 수 있음을 확인했다. 이를 통해 DCT와 Quantization RLC를 적용하는 것만으로도 표현해야하는 수의 개수가 줄어들 수 있음을 알 수 있다.
표8의 IDCT 결과에서는 고주파 성분이 상당히 표5에 비교해 상당히 소거됬음을 알 수 있다. 이를 통해 실습으로도 DCT와 Quantization 과정이 이미지의 에너지를 상당 부분 저주파 성분에 집중하게 한다는 사실을 확인할 수 있었다.
마지막으로 DCT와 Quantization 된 값을 복구한 결과 표9의 값을 얻을 수 있었는데 해당 값은 표3 즉 기존 값과 비교했을 때 육안으로 큰 차이가 없어보이는 것으로 확인되었다. 이에 대해 자세히 조사하기 위해 수식5에 나타낸 MAE(Mean Absolute Error)와 원본과 복구본의 Error를 계산하도록 하였다.


그 결과 그림6과 같은 연산결과를 얻을 수 있었다. 전체적으로 모든 Error의 크기는 8을 넘지 않았다. 또한, MAE 계산 결과 2.75로 지극히 낮아 성공적으로 복구과정이 이뤄진 것을 확인할 수 있었다.
레퍼런스
Day 63: Zig-zag
Zig-zag scan of a matrix is useful when you transform your 2D data between domains and the transformation tends to accumulate information…
medium.com
'C && C++' 카테고리의 다른 글
| [C++] 이진트리(binary tree) 전위 순회, 중위 순회, 후위 순회, 레벨 순서 순회 (0) | 2021.11.12 |
|---|---|
| [C++] Adaptive Huffman Coding(적응형 허프만 코딩) (0) | 2021.11.10 |
| [C++] Arithmetic Coding(산술 부호화) (0) | 2021.10.12 |
| OpenCV 설치하기(C++) (0) | 2021.04.30 |
| correlation 구하기 예제(대한항공, 델타항공 주가 비교) (0) | 2020.11.13 |