시험기간 때문에 최근에 업로드가 어려웠는데, 시험이 끝나 이렇게 업로드를 하니 기쁩니다.
0.서론 :
현실에서 뽑기를 하면 무작위로 상품 하나를 받게 됩니다. 이런 것을 C++로 구현할 수 있을까요? 확률은 게임 등 여러 분야에 사용되고 있습니다. 이번 시간에는 이런 확률적인 기능을 C++에서 Monte Carlo method를 이용해 구현해보도록 하겠습니다. 오늘의 목표는 monte carlo method를 이용해 원주율(파이)를 계산하는 것입니다.
1.아이디어 :
아래 그림과 같이 정사각형 안에 반듯한 원이 꽉끼여있는 상황을 상상합시다. 이 상황에서 정사각형 안에 무작위로 데이터를 생성하면, 데이터가 원안에 생성될 수도, 또는 원 밖에 생성될 수도 있습니다. 우리는 이를 통해, N(원안에 들어온 데이터의 수) / A(전체 데이터 수)를 통해 사각형의 넗이와 원의 비에 대해 실험적으로 구할 수 있습니다.
반면 이론적으로 우리는 원의 넓이가 아래식 제일 왼쪽과 같이 구해지는 것을 알고 있습니다. 그리고, 사각형의 넓이는 말할 것도 없이 이상황에서 두번째 식으로 구해지니 N(원안에 들어온 데이터의 수) / A(전체 데이터 수)에 대해 제일 오른쪽 식과 같음을 알 수 있습니다.
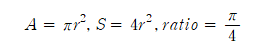

이제 느낌이 오셨을 겁니다. monte carlo_method를 이용해 무작위로 데이터를 생성한 후 이 비율을 계산하면 실험적으로 원주율 값을 알 수 있겠군요!
2. 랜덤데이터 생성 :
랜덤 데이터를 생성할 예정입니다. 우리는 비율만 구하면 원주율을 구할 수 있기때문에 제1사분면에 대해서만 데이터를 생성하도록 하겠습니다.
데이터 100개를 생성하는 코드를 기재 하겠습니다.
주석과 코드를 따라오시면 쉽게 만드실 수 있습니다.
#include <iostream>
#include <fstream>
#include <ctime>
using namespace std;
int main() {
ofstream out("pi.txt");//data를 저장하기 위한 객체
srand(time(NULL)); // 매번 시행마다 나오는 랜덤 데이터를 변경 시켜주기 위해
for (int i = 0; i < 100; i++) {//100개의 랜덤 데이터 저장
out << rand() /(float) RAND_MAX << "\t" << rand() / (float)RAND_MAX << endl;
}
}자 이제 랜덤 데이터가 생성됬습니다! 이 데이터를 이용 해 바로 N(원안에 들어온 데이터의 수) / A(전체 데이터 수)를 계산하여 원주율을 구할 수 있지만, 어떤식으로 데이터가 생성되었는지 확인하고 원주율을 확인하기 위해 python에서 데이터를 읽어들이겠습니다.
주석을 잘 적어놨으니 따라오시면 이해가 되실 겁니다.
3. 원주율 구하기
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
file = open("pi.txt","r") # C++에서 만든 데이터를 가져옴
data = file.read() # 데이터를 data변수에 써줌
data = data.split("\n") # \n으로 구분되어 잇는 데이터를 분리시켜줌
ndata = [] #data에서 x,y 를 추출한 것을 담을 변수
for i in data: # x, y 값을 추출해서 담는 과정
ndata.append(i.split("\t"))
X = []# 추출한 데이터를 다시 분리할 변수
Y = []
ndata = ndata[:-1]
for i in ndata: #데이터를 X, Y에 따로 담아줌
X.append(float(i[0]))
Y.append(float(i[1]))
cx = [] # 원을 그리기 위한 변수
cy = [] # 원을 그리기 위한 변수
incx = [] # 원안에 들어간 데이터만 담을 변수
outcx= [] #원밖에 들어갈 데이터만 담을 변수
incy= []
outcy= []
for i in range(len(X)): #원 안과 밖 데이터를 구분하는 작업
if(X[i]**2 + Y[i]**2) > 1:
outcx.append(X[i])
outcy.append(Y[i])
else:
incx.append(X[i])
incy.append(Y[i])
for i in range(102):#원을 그리기 위한 데이터
cx.append(i/100)
cy.append((1-(i/100)**2)**0.5)
plt.figure(figsize=(7, 7)) # 이미지 사이즈 결정
plt.scatter(incx,incy,c ="b",label = "in_circle") #원안 데이터 그리기
plt.scatter(outcx,outcy,c ="g",label = "out_circle") # 원밖 데이터 그리기
plt.legend()
plt.title("caculated pi = " + str(len(incy) / len(X) * 4)) #pi 값 계산
plt.plot(cx,cy,"r--") #원 그리기
plt.xlabel('x')
plt.ylabel('y')
plt.show()이 코드를 이용해서 그림을 그려내면 다음과 같은 이미지와 원주율을 얻을 수 있습니다.
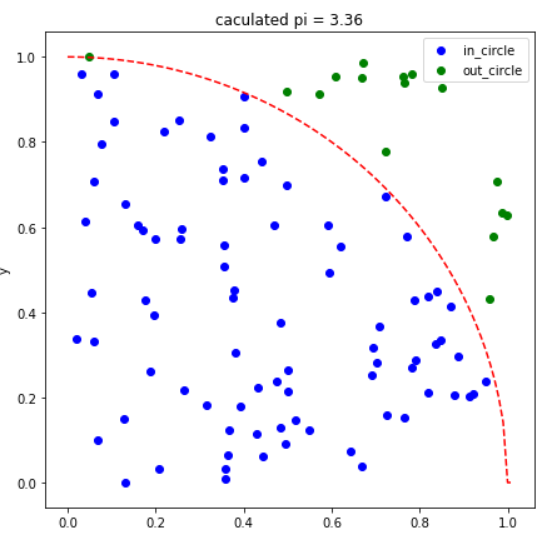
데이터 100개로 랜덤시행을 한 결과 pi값으로 3.36을 얻었습니다! 꽤 괜찮은 수치네요 불만족스러우신가요? 그러면 데이터 2000개로 랜덤시행을 진행해보겠습니다.

데이터 2000개로 진행을 하니 3.14와 매우 비슷한 원주율을 얻을 수 있습니다.
오늘은 이렇게 monte_carlo method로 원주율을 구해봤습니다.
다음에는 더 재밌는 주제로 돌아오겠습니다.
'C && C++' 카테고리의 다른 글
| [C++] Arithmetic Coding(산술 부호화) (0) | 2021.10.12 |
|---|---|
| OpenCV 설치하기(C++) (0) | 2021.04.30 |
| correlation 구하기 예제(대한항공, 델타항공 주가 비교) (0) | 2020.11.13 |
| 적분으로 물체의 포물선 운동 묘사(C++) (0) | 2020.10.17 |
| Eigen library 설치하기(C++) (2) | 2020.10.14 |