1. 1차 선형 회귀란?
1차 선형 회귀는 데이터에 대해 최대한 일치하는 y = ax + b를 찾는 것 입니다. 이번 포스팅에서는 C++에서 데이터를 이용해 a와 b 값을 찾아 데이터에 fitting 하는 것을 예시를 통해 직접 보이도록 하겠습니다. 사용되는 알고리즘은 앞서 포스팅된 경사하강법을 이용할 것이기에, 참고하시면 도움이 되실겁니다.
https://himbopsa.tistory.com/5?category=891084
경사하강법 예제(C++)
앞선 포스팅에서 함수를 시각화하는 것을 했다. 동일한 함수를 사용할 예정이고, 데이터 시각화하는 과정을 보고싶다면 참고 바란다. himbopsa.tistory.com/4 임의의 함수 시각화 하기 예제(C++) 어떤
himbopsa.tistory.com
먼저 아이디어는 다음과 같습니다.
2. 아이디어 : 각 데이터는 점이니 점과 직선사이의 거리를 계산할 수 있다. 이 거리가 최소가 되는 직선의 a와 b값을 찾아내면 최선의 1차 선형회귀를 얻을 수 있다.
3. 점과 직선 사이의 거리 계산 : ax + by + c = 0와 (x, y) 사이의 거리는 다음과 같이 나타낼 수 있습니다.

그림1의 식을 C++로 구현하면 다음과 같이 구현할 수 있다.
4. 함수와 코드들 :
float dis(float x, float y, float a, float b) {
return abs(a * x - y + b) / sqrt(a * a + 1);
}이제 경사하강법을 적용할 함수를 만들어야 합니다. 앞선 아이디어에서 설명했듯이 우리들의 목표는 거리들의 총 합을 줄이는 것입니다.. 이를 생각하면 다음과 같이 함수를 제작할 수 있다.
float f(float a, float b) {
sum = 0.0;
for (int i = 0; i < N; i++) {
sum += dis(datax[i], datay[i], a, b) / N;
}
return sum;
}이 함수에서 N은 데이터의 개수를 의미합니다. datax, datay는 각각 x좌표 y좌표를 의미하며 a, b 는 y= ax + b 에서의 a, b 값입니다. 함수를 살펴보면 앞서 만든 dis함수를 이용해 거리를 측정하고 이를 모두 합해준 후 전체 데이터 셋의 수로 나눠주는 것을 확인할 수 있습니다.
역시 경사하강법을 사용해야 하기 떄문에 미분 함수를 두개 준비해야합니다. 이 때 자유로운 변수가 a와 b이므로, 이 둘에대한 미분 함수를 준비했습니다. 코드는 아래와 같습니다.
float dfabda(float a, float b, float da) {
return (f(a + da, b) - f(a, b)) / da;
}
float dfabdb(float a, float b, float db) {
return (f(a, b + db) - f(a, b)) / db;
}
이렇게 완성된 함수를 이용해 일차 선형회기를 진행해보도록 하겠습니다.

데이터는 다음과 같이 간단한 데이터를 사용해서 작동하는지 확인 해보겠습니다. 수학적으로 봤을 때 위 데이터 셋을 통해 얻은 결과는 y = x로 기대할 수 있습니다. (맨 위의 숫자 20은 데이터의 수를 의미한다.) C++의 main에서 이를 보고 데이터가 몇개 있는지 판단하고 회귀를 진행할 것이다.
int main() {
ifstream out("simple.txt");
out >> N;
cout << N << endl;
datax = new float[N];
datay = new float[N];
for (int i = 0; i < N; i++) {
out >> datax[i] >> datay[i];
cout << datax[i] << " " << datay[i] << endl;
}
float a0 = 0, b0 = 0;
int iteration = 0;
float eta = 0.0001;
float psi = 0.005;
float da = 0.01;
float db = 0.01;
float a1 = 3, b1 = 10;
while (EE(a0, b0, a1, b1) > eta && iteration < 1000000) {
a0 = a1;
b0 = b1;
a1 -= psi * dfabda(a0, b0, da);
b1 -= psi * dfabdb(a0, b0, db);
iteration++;
}
cout << " y = " << a1 << "x + " << b1 << endl;
cout << iteration << "-th E = " << EE(a0, b0, a1, b1) << endl;
return 0;
}5. 결과 :

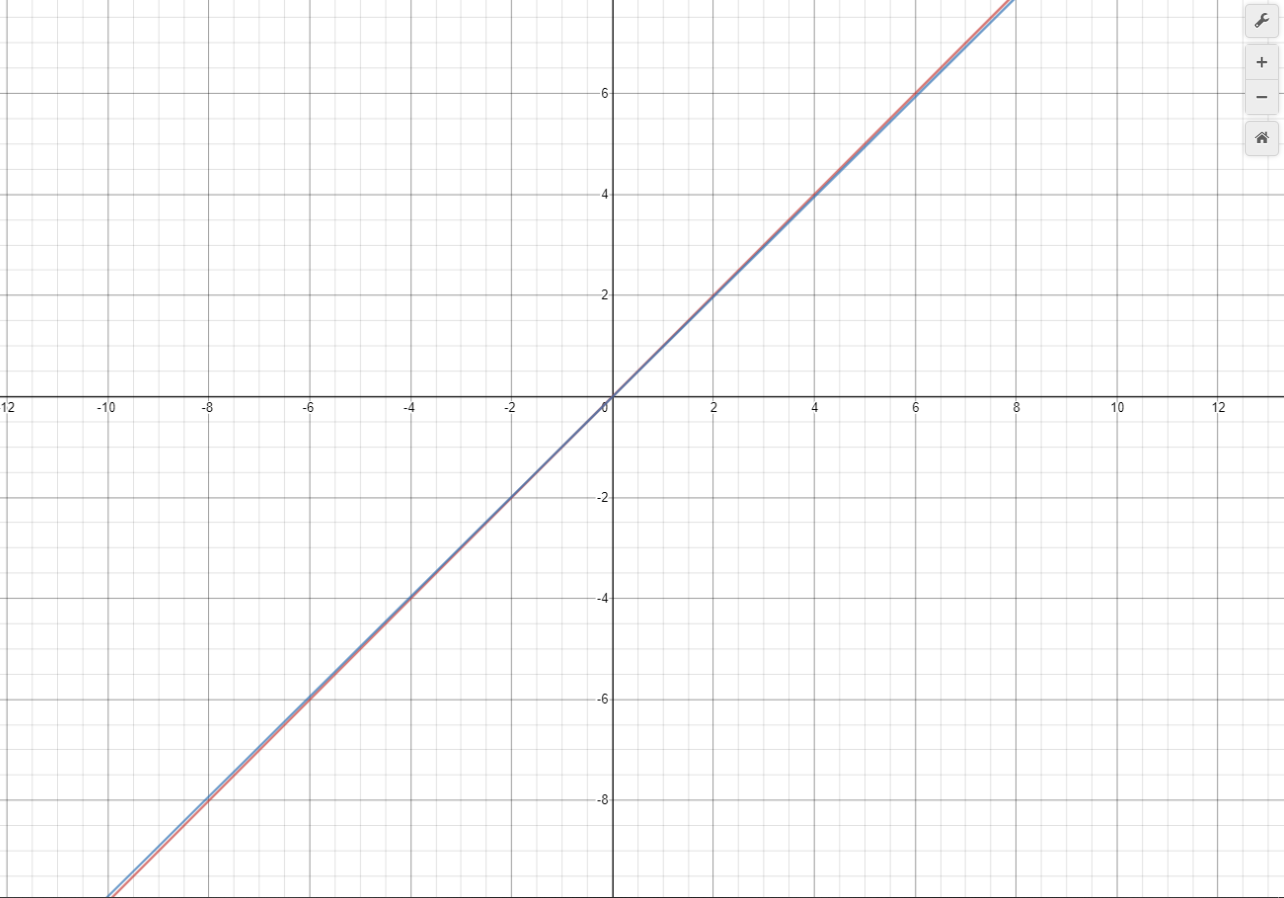
결과적으로 y = 0.989152x -0.00591446을 획득할 수 있었습니다. 이는 앞서 기대한 y = x와 거의 비슷한 수치로 만족스럽습니다. 그림4를 보면 이미지 적으로도 두 선이 거의 일치하는 것을 관찰할 수 있습니다.이렇게 일차선형회기를 하는법을 알아봤습니다. 다음에는 matrix를 이용한 1차선형회기를 다루겠습니다.
'C && C++ > C++ X 머신러닝' 카테고리의 다른 글
| 다항회귀 예제(C++ with eigen library) (0) | 2020.10.17 |
|---|---|
| 경사하강법 예제(C++) (0) | 2020.10.12 |
| 임의의 함수 시각화 하기 예제(C++) (0) | 2020.10.12 |