안녕하세요~~!! 다시 돌아온 AstroPeguin입니다!
기말고사가 끝나고 종강을 해서 다시 글을 쓰게 되었습니다.
오늘은 식현상을 이용한 외계행성의 검출과 물리량을 측정하는 과정에 대해 알아보겠습니다.
인간의 과학은 지구의 역사 중 찰나의 순간 동안 빠르게 발전되어왔고, 급기야 지구를 벗어나 우주를 영역으로 한 과학이 발전하고 있습니다. 그리고 이러한 천문학 빠른 속도로 발전되고 있습니다. 망원경을 통해 태양과 행성, 달의 움직임을 분석하던 인간이 이제는 거대한 항성이나 은하의 생성 메커니즘을 이해하고, 암흑물질과 암흑에너지의 존재로 우주의 과거와 현재, 미래를 추측하기도 합니다. 이처럼 뛰어난 지성을 가지는 인간은 한 가지 의문에 빠졌을 것입니다. “우주에서 인간 이외의 생명체가 살지 않을까?”, “우주에도 생명체가 살 수 있는 생명체가 있지 않을까?”라는 생각이 들게 되고, 아직은 많이 발전하고 알려지지 않았지만 천문생물학과 외계행성탐사라는 분야가 탄생하게 됩니다.

외계행성을 찾아내기 위해 최초로 시작된 mission은 바로 [Kepler Mission]입니다. 케플러 미션은 외계행성과 모항성의 식현상을 이용한 검출방법을 통해 외계행성을 찾아내고자 하였습니다. 케플러 망원경은 광학 CCD를 이용하여 외계 항성들의 flux 변화를 관측하도록 제작되었습니다. 그리고 이를 보정한 PDCSAP flux와 관측한 줄리안데이(BJD)의 정보를 fits파일로 제공합니다. 그리고 천문학자들은 flux와 줄리안데이, 즉 시간-밝기 대해 표현하여 light curve를 그리고 분석하여 수 많은 외계행성의 존재들을 알아냈습니다.

식현상을 이용한 검출 방법의 원리에 대해 간단히 설명 드리겠습니다.
외계행성과 모항성이 식현상을 일으키게 된다면 외계행성의 면적만큼 모항성의 밝기는 감소할 것입니다. 이를 시간-밝기인 광도 변화 곡선으로 나타낸다면, 밝기가 감소하는 구간을 통해 외계행성의 존재를 확인할 수 있습니다.
외계행성이 모항성 주의를 주기적으로 돌면서, 식현상을 하게 되면 Lightcurve(광도곡선)에서는 광도(flux)에 관한 값이 주기적으로 감소했다가 증가하는 구간이 생길 것입니다. 이 때 주의할 점은 그려지는 광도곡선이 외계행성의 광도곡선이 아닌 모항성의 광도곡선이라는 점을 항상 명시해야 합니다.
광도곡선이 감소하는 두 구간 사이의 시간을 알아내면, 그것이 외계행성의 공전주기가 되고
광도곡선이 감소하는 시간을 측정하면, 외계행성의 식현상이 진행되는 시간이 되고
광도곡선이 원래 밝기에 비해 감소하는 비율을 구하면, 이를 통해 외계행성의 크기를 알 수 있으며
광도곡선의 정보들로 중력=구심력의 방정식을 푼다면 외계행성의 공전궤도 반지름을 알아낼 수 있습니다.

자 그렇다면 이제 저와 함께 외계행성의 데이터를 얻는 과정과 파이썬을 이용해 외계행성의 공전주기, 면적, 공전궤도 반지름을
구하는 여정을 떠나보도록 하겠습니다!!
제가 앞서 말씀드린 것 처럼 외계행성을 검출하기 위한 최초의 미션은 [케플러 미션]입니다.
케플러 우주망원경을 통해 관측된 외계행성을 검출하기 위한 정보는 모두 케플러 아카이브에 담겨있습니다.
우선 케플러 아카이브에 들어가 데이터를 구해보도록 하겠습니다.
Kepler
Kepler Mission Homepage
archive.stsci.edu

케플러 아카이브에서는 주로 lightcurve를 그리기 위한 데이터와 코드를 제공하거나, 데이터에 대한 접근방식 뿐만 아니라 외계행성계의 픽셀이미지나, 실제 사진 등을 나타내는 방법 및 코드를 제공하기도 합니다.
우선 이러한 얘기는 미루어 두고 케플러 아카이브에 들어가셔서 스크롤을 내리면 다음과 같은 화면이 나타납니다.
이 화면에서 EXO.mast라는 곳을 클릭하셔서 들어가시면 됩니다.

검색창에 원하는 외계행성의 이름을 쓰신다면 다음과 같이 외계행성에 관련된 데이터를 얻을 수 있습니다.
데이터를 검색한 후 Waveband가 optical(가시광선), Product가 timescale, Filters가 KEPLER인 데이터를 찾아 맨 오른쪽의 주황글씨를 클릭하여 다운 받은 후 압축을 해제합니다. (fits파일 형식인 것 확인하고 다운 받기!)

이제 파이썬으로 들어가 코드를 작성하도록 하겠습니다~~~~
저희가 사용할 천체는 케플러 우주망원경이 2010년경 최초로 발견한 의미 있는 외계행성들 중 하나인 kepler-4b입니다.
우선 사용할 numpy, matplotlib, astropy 등의 기능들을 import합니다. 그 후 파일을 불러오고 fits.info()를 통해 데이터의 형식을 봅니다.
from astropy.io import fits
from astropy.table import Table
import matplotlib.pyplot as plt
import numpy as np
data = "kplr011853905-2009131105131_llc.fits"
fits.info(data)
케플러 망원경의 데이터 형식 본다면 ‘LightcurveHDU’라고 쓰여 있는 곳이 있는데 케플러 프로젝트가 모두 광도곡선을 그려 식현상 방법을 이용하여 외계행성을 검출할 목적을 가지고 있음을 알 수 있습니다. 저희는 이 지점의 데이터를 이용할 것입니다. 추가로 만약 이미지를 표출하고 싶다면 밑의 ImageHDU의 데이터를 이용하면 됩니다.
이제 데이터의 header[0], PrimaryHDU를 출력하여 관측기기와 관측 대상에 관한 정보를 얻을 것입니다.
with fits.open(data) as hdulist:
header1 = hdulist[0].header
# lightcurve에 관한 정보는 두 번째에 담겨있으므로
print(repr(header1[:]))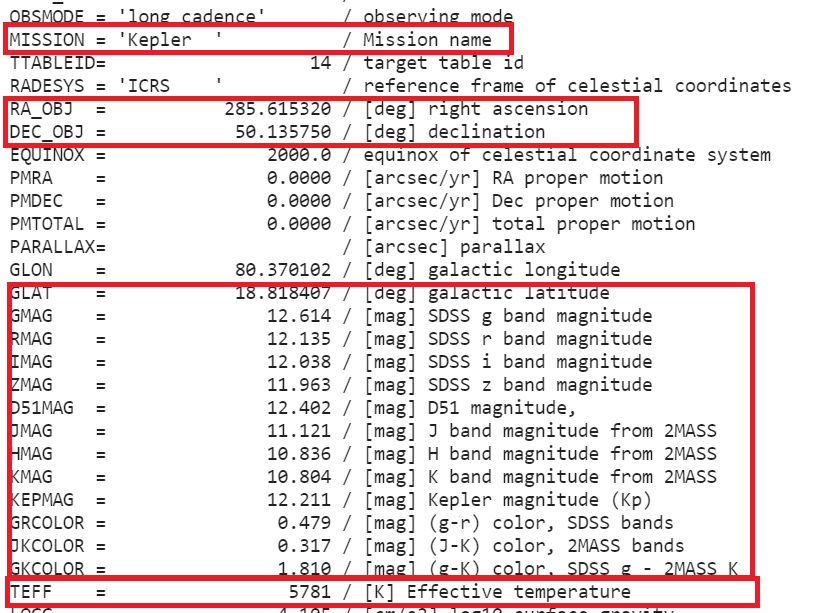
출력된 값들을 보시면 관측 미션, 해당 외계행성의 모항성의 적경과 적위, 각각의 필터로 관측한 광도, 표면 온도 등의 정보들이 담겨있음을 알 수 있습니다.
그 후 데이터의 header[1], LightcurveHDU를 출력하여 시간-광도 그래프를 그리기 위한 시간 (time scale)에 관한 정보를 얻어낼 것입니다. 이 부부분은 위의 코드에서 header[0]을 header[1]로 바꿔주시면됩니다.
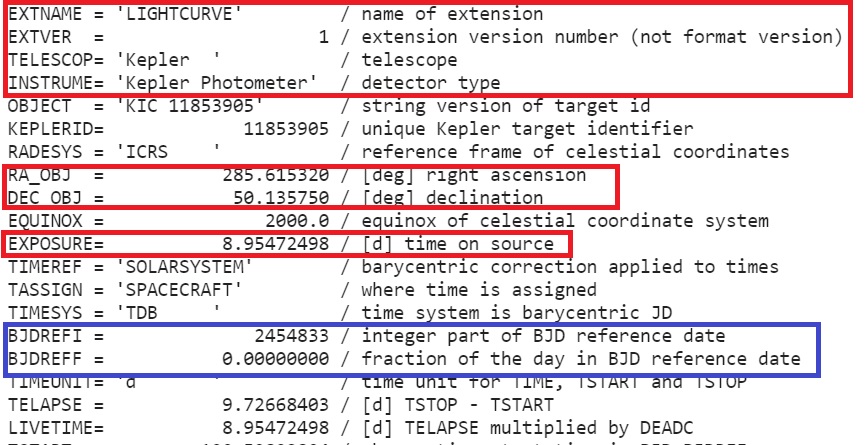
이를 출력하면 아까의 PrimaryHDU보다 훨씬 자세하게 미션의 이름과 관측기의 이름, 적경/적위, 노출시간, 그리고 저희가 원하는 시간값인 줄리안데이로 표현된 BJDREFI와 BJDREFF를 얻을 수 있습니다.
이제 앞서 보았던 데이터 형식 중에서 ‘LightcurveHDU’의 데이터를 불러오는 과정을 거쳐 본격적으로 lightcurve를 그려보도록 하겠습니다. 우선 데이터들을 Talble형식으로 불러와 광도(flux) 및 날짜 데이타의 이름을 확인합니다.
with fits.open(data) as hdulist:
binaryext = hdulist[1].data
binarytable = Table(binaryext)
binarytable[0:5]
저희가 사용할 flux(밝기)의 값은 오차를 보정한 PDCSAP_FLUX입니다.
그리고 원래의 시간인 TIME 또한 LightcurveHDU에서 불러온 BJDREFI, BJDREFF와 더해줌으로써 오류가 없는 정확한 시간을 구현할 예정입니다.
저희가 사용할 데이터들을 찾았으니 이제 사용항 데이터들을 선언하여 lightcurve를 그려보겠습니다.
with fits.open( data or header ) as hdulist: 구문에서 data 또는 header를 지정하여 이 구문을 쓰면 data 또는 header에있는 한 데이터를 불러오는 작업을 수행할 수 있습니다.
예를 들어 with fits.open( data or header ) as hdulist: 구문 뒤에 bjdreif=hdulist[1].header['BJDREFI'] 구문을 작성하면 bjdreif를 header의 BJDREFI에서 불러와서 선언하여 자유롭게 사용할 수 있습니다.
이처럼 시간에 관한 factor들과 flux에 관한 factor인 PDCSAP_FLUX를 선언하여 matplotlib.pyplot을 통해 시간-광도의 lightcurve(광도곡선)을 그려줍니다.
with fits.open(data) as hdulist:
header1 = hdulist[1].header
with fits.open(data) as hdulist:
binaryext = hdulist[1].data
binarytable = Table(binaryext)
with fits.open(data, mode="readonly") as hdulist:
# Read in the "BJDREF" which is the time offset of the time array.
bjdrefi = hdulist[1].header['BJDREFI']
bjdreff = hdulist[1].header['BJDREFF']
# Read in the columns of data.
times = hdulist[1].data['time']
pdcsap_fluxes = hdulist[1].data['PDCSAP_FLUX']
pdcsap_fluxes_err = hdulist[1].data['PDCSAP_FLUX_ERR']
# Convert the time array to full BJD by adding the offset back in.
bjds = times + bjdrefi + bjdreff
real_flux = pdcsap_fluxes-pdcsap_fluxes_err
plt.figure(figsize=(9,4))
plt.plot(bjds, real_flux, 'black')
plt.title('Kepler-4b Light Curve', fontsize = 20)
plt.legend()
plt.xlabel('Time (days)', fontsize = 15)
plt.ylabel('Flux (electrons/second)', fontsize = 15)
plt.show()
이 때 항상 알아둬야 할 점은 이 광도변화 그래프는 외계행성인 kepler-4b의 광도변화가 아닌 모항성 kepler-4의 광도곡선이라는 점을 항상 알아둬야 합니다. 그래프를 살펴보면 광도가 주기적으로 일정수치만큼 비교적 크게 감소하는 것을 볼 수 있습니다. 이로 미루어보아, 모항성을 가리는 무언가가 모항성 주변을 공전하고 있다고 추론하게 됩니다. 바로 외계행성이 존재한다는 사실을 다음과 같이 알아낸 것입니다.
이를 자세하게 보기 위해 외계행성의 식현상이 일어나는, 광도가 급격하게 줄었다가 늘어나는 구간들 중 하나를 잘라내보겠습니다. 잘라내기 위해서 np.where구문을 사용하여 식이 시작되는 줄리안데이와 식이 종료되는 줄리안데이를 각각 지정하여 그 사이의 값들만 표출하였습니다.
# 배열을 특정 범위로 잘라내기
import numpy as np
a = 2.4549e6+56.35 #임의 지정
b = 2.4549e6+56.85 #임의 지정
arange = np.where((bjds>=a)&(bjds<=b))[0] #범위 지정
cut_flux = real_flux[arange] #범위안의 내용으로 잘라내기
cut_bjd = bjds[arange]
plt.figure(figsize=(12,6))
plt.plot(cut_bjd, cut_flux, c='black')
plt.plot(cut_bjd, cut_flux, 'o', c='orange', markersize=5)
plt.title('Kepler-4b Light Curve', fontsize=20)
plt.xlabel('Time (days)', fontsize=15)
plt.ylabel('Flux (electrons/second)', fontsize=15)
plt.show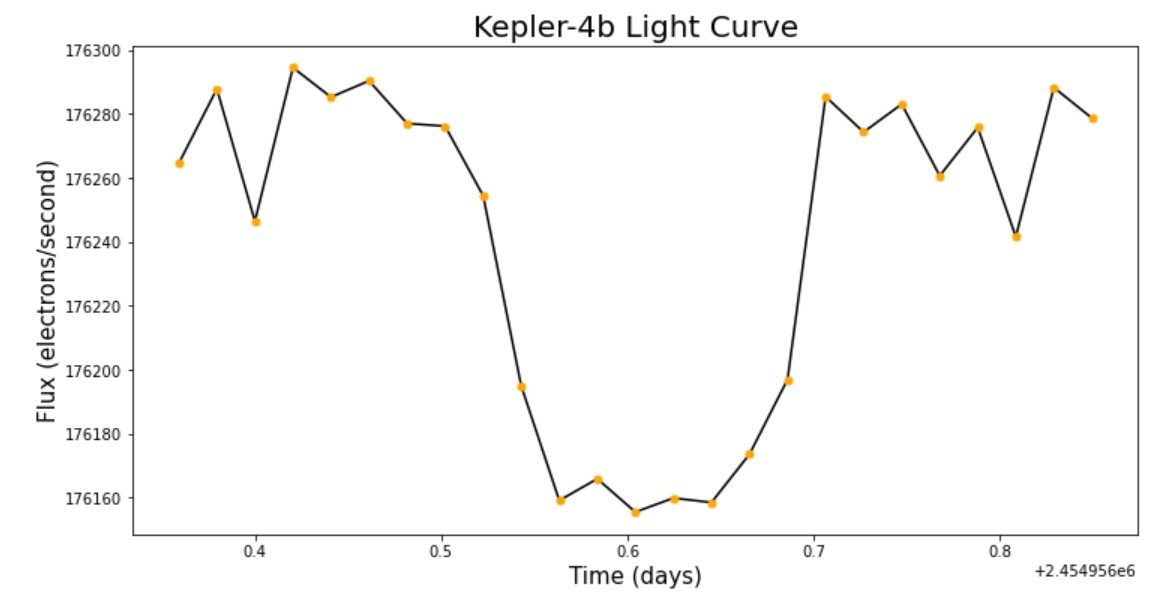
이제 외계행성의 존재를 확인했으니 kepler-4b의 모든 물리량에 대해 파해쳐보겠습니다.
우선 외계행성이 식을 일으키는 중이라고 가정할 수 있는 flux값을 설정합니다.
저는 광도곡선 그래프에서 식 현상이 일어날 것으로 예상되는 세 구간을 잘라내어
if구문을 사용하여 실제 flux값이 일정 flux값(eclipse_flux = 176200) 미만으로 내려갈 때 식현상이 일어났다고 가정하고
그 때에 해당하는 모든 BJD(시간)값들을 새로운 배열로 append구문을 통해 각각 받아들일 것입니다.
그리고 모든 각각의 식현상 배열 시간값들을 더한 후 이를 각각의 배열들의 개수로 나누어주면,
식현상이 일어난 평균적인 한 시간 지점을 특정할 것입니다. (이는 평균을 냈으므로 각각의 식현상에서 광도의 최솟값에 해당하는 날짜(시간)과 일치합니다.)
그리고 각각의 구해진 시간들 사이, 식현상들 사이의 시간을 평균내어 공전주기를 구합니다.
# 외계행성의 공전주기 구하기
eclipse_flux = 176200
eclipse_bjds1 = []
eclipse_bjds2 = []
eclipse_bjds3 = []
for i in range(len(real_flux)):
if real_flux[i]<eclipse_flux:
if bjds[i]<2454958:
eclipse_bjds1.append(bjds[i])
eclipse_moment1 = sum(eclipse_bjds1)/len(eclipse_bjds1)
elif bjds[i]>2454958 and bjds[i]<2454960:
eclipse_bjds2.append(bjds[i])
eclipse_moment2 = sum(eclipse_bjds2)/len(eclipse_bjds2)
elif bjds[i]>2454962:
eclipse_bjds3.append(bjds[i])
eclipse_moment3 = sum(eclipse_bjds3)/len(eclipse_bjds3)
ecilpse_period = ((eclipse_moment2-eclipse_moment1) + (eclipse_moment3-eclipse_moment2) + (eclipse_moment3-eclipse_moment1)/2)/3
print('Exoplanet(Kepler-4b) revolution period : ', ecilpse_period, 'days')이를 출력하면 EXO.MAST에 제공되는 이론값과 제가 출력한 공전주기의 값이 거의 유사한 것을 알 수 있습니다.
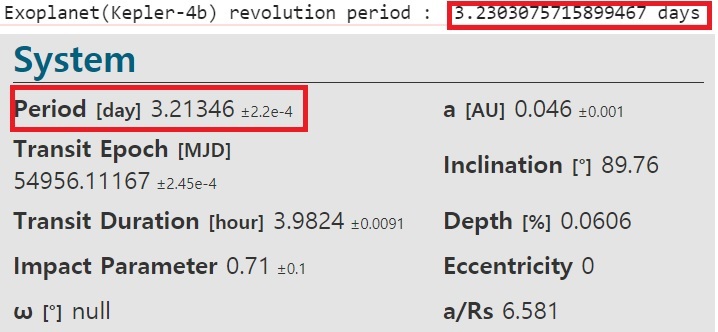
다음으로는 외계행성 kepler-4b의 면적과 반지름을 구해보겠습니다.
이 때 사용되는 법칙은 스테판-볼츠만 법칙입니다.
이 법칙은 별의 밝기가 별의 면적과 온도의 네제곱에 비례한다는 내용입니다.
즉, 스테판-볼츠만 법칙을 외계행상의 식현상으로 인한 별의 밝기 감소한 비율이 별의 면적이 감소한 비율과 같다는 뜻이라고 응용할 수 있습니다. 그리고 별의 면적이 감소한 비율이 외계행성과 모항성의 면적 비율과 같으므로
모항성의 면적, 모항성의 광도 변화 비율을 안다면 외계행성의 면적과 반지름을 구할 수 있습니다.
우선 header에 모항성인 kepler-4의 반지름을 태양의 반지름으로 나눈 몫의 값이 RADIUS에 담겨있으므로 이를 선업하여 불러옵니다. 그리고 이를 태양의 반지름 및 면적과 곱하면 모항성의 면적과 반지름을 구할 수 있습니다.
다음으로는 식현상이 일어났을 때의 밝기변화를 구하기 위해 주기를 구할 때와 비슷한 코드를 사용합니다. 다만 불러오는 값이 BJD가 아닌 flux값입니다. if구문을 사용하여 각각의 식현상 구간을 잘라내어 식현상의 flux보다 작은 모든 flux값을 받아들입니다. 그리고 모항성의 밝기 변화 비율을 구하기 위한 이들의 최솟값을 구하고 평균을 내주어 최소 밝기값을 구합니다.
마지막으로 평균적인 모항성의 배경밝기를 설정하고 앞서 구한 최소 밝기를 나눈 후 1에서 그 값을 빼주어 실제 밝기의 변화 비율을 구하고 이 비율을 모항성의 면적에 곱해줌으로써 외계행성의 면적을 구합니다. 그리고 면적을 통해 반지름을 구하고 이를 지구의 반지름 또는 목성의 반지름과 비교하여 출력합니다.
# 모항성의 크기 구하기
with fits.open(data, mode="readonly") as hdulist:
radius_raito = hdulist[0].header['RADIUS']
sun_radius = 6.96*1e5 # km unit
stellar_radius = radius_raito*sun_radius
stellar_area = np.pi*(stellar_radius**2)
print('Radius of Kepler-4 : ', stellar_radius, 'km')
print('Area of Kepler-4 : ', stellar_area, 'km^2')
# 식현상이 일어났을 때 밝기
flux1 = []
flux2 = []
flux3 = []
for i in range(len(real_flux)):
if real_flux[i]<eclipse_flux:
if bjds[i]<2454958:
flux1.append(real_flux[i])
elif bjds[i]>2454958 and bjds[i]<2454960:
flux2.append(real_flux[i])
elif bjds[i]>2454962:
flux3.append(real_flux[i])
min_flux1 = min(flux1)
min_flux2 = min(flux2)
min_flux3 = min(flux3)
avg_min_flux = (min_flux1+min_flux2+min_flux3)/3
print('Average of minimum flux : ', avg_min_flux)
# 밝기 변화를 통한 외계행성 크기 구하기
background_flux = 176298
change_of_flux = avg_min_flux/background_flux #밝기변화 비율
ratio_of_area = (1-change_of_flux)
exoplanet_area = ratio_of_area*stellar_area
exoplanet_radius = np.sqrt(exoplanet_area/np.pi)
#구한 값 출력
print('Area change raito : ',ratio_of_area)
print('Area of Kepler-4b : ', exoplanet_area, 'km^2')
print('Area of Kepler-4b : ', exoplanet_area/(np.pi*(69911)**2), 'Area of jupiter')
print('Area of Kepler-4b : ', exoplanet_area/(np.pi*(6400)**2), 'Area of earth')
print('Radius of Kepler-4b : ', exoplanet_radius, 'km')
print('Radius of Kepler-4b : ', exoplanet_radius/69911, 'Radius of jupiter')
print('Radius of Kepler-4b : ', exoplanet_radius/6400, 'Radius of earth')
print('Error of radius : ', (4.71-3.88)/3.88*100, "%")
저는 오차율이 21%로 비교적 크게 나왔지만, 여러분들은 평균을 구하는 방법이나, flux를 추출하는 방법을 알맞게 조절한다면 오차를 줄일 수 있으실 겁니다!!
그리고 비교를 위한 이론값은 EXO.MAST에서 원하는 외계행성을 검색하면 맨 왼쪽에서 보실 수 있습니다.
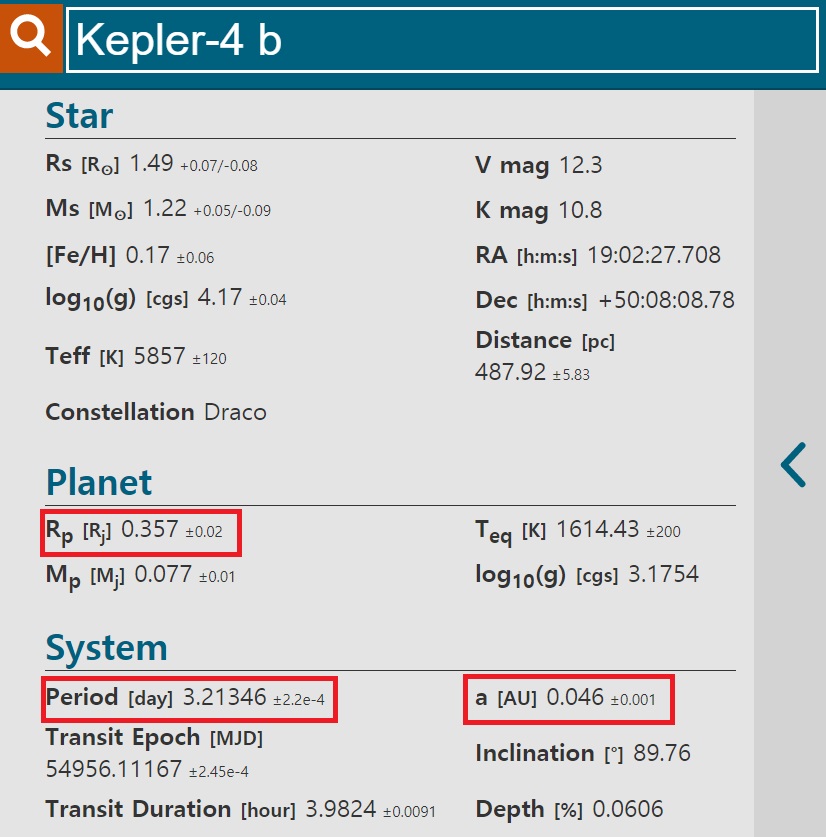
이제 여정의 끝자락에 왔습니다...ㅠ-ㅠ
공전궤도의 반지름을 구하기 위해 저는 중력=구심력이라는 간단한 방정식을 세웠습니다.
그런데 구심력인 mv^2/r에서 v를 알 수 없었는데,
저는 이 문제점에서 한가지 개념을 적용시켰습니다.
바로 v = wr입니다. 속도는 각속도와 거리의 곱이라는 사실말입니다.
이를 통해 공전 궤도 반지름을 유도하면 다음과 같습니다.

우선 식현상이 일어나는 구간의 시간간격을 구하고, 각속도의 정의를 통해 각속도를 구합니다.
그 후 중력=구심력 공식에 필요한 모항성 kepler-4의 질량, 중력상수 등을 선언하고
제가 구한 공식에 각각 대입하여 공전궤도 반지름을 구하고 AU단위로도 나타내었습니다.
# 공전궤도 반지름 구하기
#1 각속도 구하기
eclipse_time = 0.206 # 식현상을 하는데 걸리는 시간(일)
eclipse_angle = (2*np.pi*eclipse_time)/ecilpse_period
angle_velocity = 2*np.pi/(ecilpse_period*24*60*60)
# 3.23 : 2pi = 0.206 : angle
# 각속도 = 2pi/공전주기
# 중력=구심력을 통한 반지름 측정
sun_mass = 1.98*1e30 # kg
stellar_mass = 1.117*sun_mass
G = 6.67*1e-11
AU = 1.5e11 # m
# r^3 = root(GM/w^2)
orbit = np.cbrt(G*stellar_mass/angle_velocity**2)
print('Radius of orbit : ',orbit/AU,'AU')
print('Error : ',100.0*(0.04558-orbit/AU)/0.04558,'%')
마지막으로 케플러 아카이브와 EXO.MAST에서 케플러 우주망원경을 통해 관측한 모항성의 시간-광도 데이터를 통해 Lightcurve를 그려보았습니다. 그리고 광도곡선을 분석하여 외계행성의 존재를 알아내고, 외계행성의 공전주기, 반지름 및 면적, 그리고 공전궤도 반지름을 구해보았습니다.
저희가 출력한 값들과 이론값들이 거의 일치하였지만, 일부 아쉬운 결과를 보이는 곳도 있었습니다. 저는 제 나름대로의 방법을 사용한 것입니다. 여러분도 저의 방법을 그대로 따라가긴 보단 수 많은 생각과 과정을 거치고, 코드에 대한 이해를 거쳐 여러분만의 방법으로 제가 만든 오차들을 모두 줄이시길 바랍니다!!!
같은 요리라도 수 많은 조리법이 있듯이, 같은 Lightcurve를 분석하더라도 수 많은 코드와 방법으로 해결할 수 있습니다. 저는 저의 방법을 공유한 것이고, 나머지는 여러분의 몫입니다.
여러분 스스로 생각하고 발전시켜야 코딩을 이용한 천문학이 다양해지고 미약하게나마 발전할 수 있다고 생각합니다.
이상 외계행성탐사 여정을 마치겠습니다^^