릿지 회귀 예제(파이썬/python)

지난 포스팅에서 정규방정식을 이용해 일반화 모델을 만들었습니다. 못보신 분들을 위해 아래에 링크를 걸어두도록 하겠습니다.

himbopsa.tistory.com/11?category=891086

1차 선형회귀 예제(파이썬 정규 방정식)

 이 때 저희 가 얻은 theta 값은 

[[1.53371047] [1.98419393]] 으로 실제 데이터 [[1],[2]]와 근사하지만, theta_0 의 결과가 조금 실망스러웠습니다. 그 때 포스팅에서 규제를 추가하면 개선될 수 있을 것이라고 제가 말씀드렸는데요, 릿지 회귀를 통해 규제가 있는 상황에서 theta가 어떻게 구해지는지 알아봤습니다. 함수는 동일 함수를 이용할 예정이고 noise의 정도도 동일하게 할 생각입니다. 시작하기전에 함수를 발생하는 코드를 먼저 적고 가는 것도 좋을것 같군요.

X =5 * np.random.rand(100,1) 
Y = 2 * X +1 + np.random.rand(100,1)

 np.random.rand(m, n) : "m by n size의 성분은 random한 행렬을 만들겠다는 method"과 같은 여러 method들이 나오는데 이는 위의 링크로 가시면 자세한 설명이 있습니다.!

그림1. 규제가 없는 상황에서 일반화 모델

 0) Ridge란?

ridge는 일반적인 MES 함수에 rdige 규제항을 추가해 만든 모델을 의미합니다. 식으로는 다음과 같이 나타낼 수 있습니다.

그림2, 릿지회귀 비용 함수

 이 비용함수 J를 최소화 하는 방향으로 모델은 학습을 진행할 것입니다. 이제 기본적인 원리에 대해 알아봤으니 코드를 작성해 실제 규제를 해보도록 하겠습니다.

 

1)Ridge 회귀 pyrhon 코드

 사용된 라이브러리 부터 적고 가도록 하겠습니다. 코드를 동작시켜보고 싶으신 분은 꼭! 라이브러리가 설치되어있는지 확인해 주세요.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge

 라이브러리를 importing 해주셨으면 정말 간단한 전체 코드에 대해서 보겠습니다.

ridge_reg = Ridge(alpha = 0.25)
ridge_reg.fit(X,Y)
a = ridge_reg.predict([[0]])
b = ridge_reg.predict([[5]])
print((b[0] - a[0]) / 5)
print(a[0])

 먼저 Ridge객체를 규제 alpha = 0.25로 만들어 줬습니다. 그리고 이를 X,Y 데이터에 대해서 fitting 해줬습니다. 그리고 아래 print를 통해서 theta 값에 대해서 알아봤습니다.

 theta :

[2.00642603] [1.46870303]

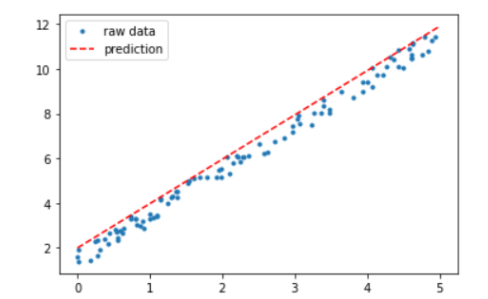
 확실이 이전 결과와 비교해서 개선이 되었네요! 이를 그림을 그려서 비교해 보겠습니다. 

plt.plot(X, Y, "b.",label = "data")
plt.plot([0,5],[a[0],b[0]],"r--",label = "prediction")

plt.title("Ridge")
plt.legend()
plt.show()

그림3, ridge 규제를 적용해 만든 일반화 모델

 

 그림으로 비교하니 더 명확하게 ridge 규제가 있는 모델이 일반화가 잘되었네요. 이렇게 Ridge 규제에 대해서 알아봤습니다. 다음 시간에는 Rasso 회귀에 대해서 포스팅 하겠습니다. 감사합니다.